答え　∠DAB=54°

証明

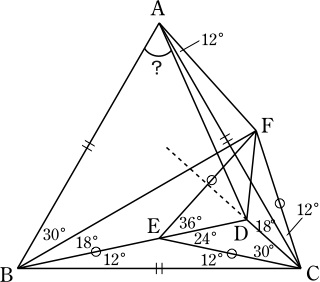BD上に ∠BCE=12°となるように点Eをとると， ∠ECD=60°-∠BCE-∠DCA=30°．
また，直線CDに対してEと対称の位置に点Fをとると， CE=CF， ∠DCF=∠ECD=30°で， ∠ECF=60°となるので， △CFEは正三角形で， EC=EF．
∠ACF=∠DCF-∠DCA=12°， ∠DEC=∠BCE+∠DBC=24°， ∠DFE=∠FED=60°-24°=36°， ∠BDF=∠EDF=180°-36°-36°=108°．
また， ∠EBC=12°=∠BCEより， EB=EC=EFなので， Eは△BCFの外心であり， ∠FBC=∠FEC/2=30°．
△ABCは正三角形なので，２点A,Cは直線BFに対し互いに対称の位置にあることになり， ∠FAC=∠ACF=12°．
∠FAB=12°+60°=72°．
∠FAB+∠BDF=180°なので，四角形ABDFは円に内接し， ∠FAD=∠FBD=30°-12°=18°．
∠DAB=∠FAB-∠FAD=54°．

別解１

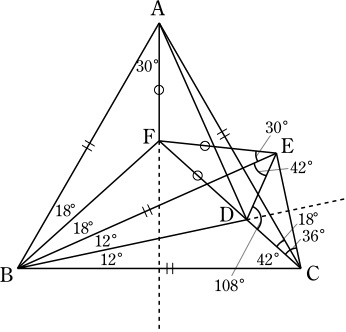∠BCD=42°．
直線BDを軸としてCと対称の位置に点Eをとり， ∠BACの二等分線と直線CDの交点を点Fとおく．
BDについての対称性より， ∠EBD=∠DBC=12°， ∠DEB=∠BCD=42°， BC=BE．
また， ∠BDC=∠BDE=126°より， ∠EDC=108°．
∴ ∠FDE=180°-∠EDC=72°．
一方，AFについての対称性より， ∠ABF=∠ACF=18°．
∠EBF=60°-∠ABF-∠EBD-∠DBC=18°=∠ABF， BE=BC=BAより， △ABF≡△EBF．
∴ ∠BEF=∠BAF=30°， FA=FE．
∠DEF=∠BEF+∠DEB=72°=∠FDEより， FD=FE=FA．
∠AFD=180°-∠FCA-∠CAF=180°-18°-30°=132°より， ∠DAF=∠FDA=24°．
∠DAB=∠DAF+∠BAF=54°．

別解２

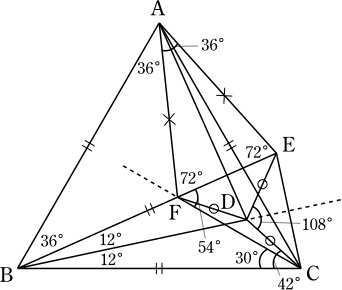∠BCD=42°．
直線BDを軸としてCと対称の位置に点Eをとり， ∠BCAの二等分線と線分BEの交点を点Fとおく．
BDについての対称性より， ∠EBD=∠DBC=12°， BC=BE， DC=DE．
∠BCE=∠CEB=78°， ∠DCE=∠BCE-∠BCD=36°．
∴ ∠EDC=180°-2∠DCE=108°．
∠EFC=∠FBC+∠BCF=54°．
DC=DE， ∠EDC=2∠EFCより， Dは△FCEの外心で， DE=DF．
また，BA=BC=BE， ∠ABE=60°-∠EBD-∠DBC=36°より， ∠BEA=∠EAB=72°．
ここで，CFについての対称性より， ∠FAB=∠ABF=36°．
∴ ∠AFE=72°， ∠EAF=36°．
∠FEA=∠AFEより， AE=AF．
これと， DE=DFより， △AED≡△AFD， ∠EAD=∠FAD=18°．
∠DAB=∠FAB+∠FAD=54°．

別解３

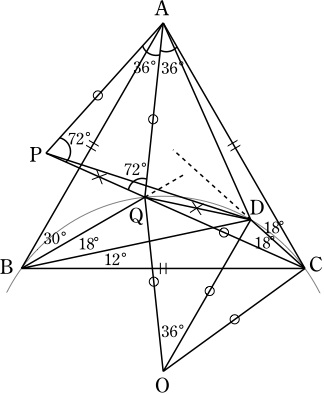直線CDを軸としてAと対称の位置に点Pをとり， ∠ABCの二等分線と線分CPの交点を点Qとおく．
CDについての対称性より， ∠PCD=∠DCA=18°， ∠CAP=∠APC=72°．
BQについての対称性より， ∠CAQ=∠QCA=36°， AQ=CQ．
∠PQA=72°=∠APQより， AP=AQ， ∠QAP=36°．
また， ∠QBD=∠QBC-∠DBC=18°=∠QCDより，四角形QBCDは円に内接する．
四角形QBCDの外接円の中心をOとすると， ∠QOC=2∠QBC=60°より， △QOCは正三角形で， OQ=CQ=AQ．
∠QOD=2∠QBD=36°=∠QAP， OD=OQ=AQ=APより， △APQ≡△ODQで， QP=QD．
また， ∠DQC=∠DBC=12°より， ∠DPQ=∠QDP=6°．
CDについての対称性より， ∠CAD=∠DPQ=6°．
∠DAB=60°-∠CAD=54°．

別解４

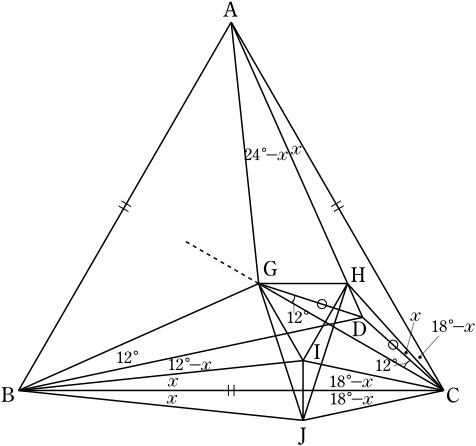DG=DC，∠CDG=156°となるような二等辺三角形DGCを，直線CDから見てAと逆側に作る．
∠GCD=∠DGC=12°， ∠GCA=12°+18°=30°より， CGは∠BCAの二等分線である．
また，∠DGC=∠DBCなので，四角形GBCDは円に内接し， ∠GBD=∠GCD=12°， ∠GBC=24°．
ここで，∠CAD=xとおく．
直線CGに対して点Dと対称の位置に点D'をとると， D'は明らかに △DBCの内部にあるので， ∠D'BC＜∠DBC=12°であり， ∠D'BC=∠CAD=xなので， x＜12°．
x＜∠DCAなので，線分DA上に ∠DCH=xとなるような点Hをとることができる．
また，直線CGに対してHと対称の位置に点Iを，直線BCに対してIと対称の位置に点Jをとる．
対称性より，△HCA≡△ICB≡△JCBであり， ∠CBJ=∠CBI=∠CAH=x， ∠JCB=∠ICB=∠HCA=18°-x．
また，CGについての対称性より， GH=GI， ∠GAH=∠GBI=24°-x．
ここで，△DCH∽△DACなので， DH・DA=DC2 であり， DC=DGより，DH・DA=DG2 となるので， △DGH∽△DAG．
∴ ∠HGD=∠GAD=∠GAH=24°-x．
∠HGC=∠HGD+∠DGC=36°-x．
CGについての対称性より， ∠HGI=2∠HGC=72°-2x， ∠GIH=∠IHG=54°+x．
一方，CH=CI=CJより，H,I,JはCを中心とする円周上にある．
∠ICH=60°-2(18°-x)=24°+2x， ∠JCH=60°-∠HCA+∠JCB=60°より， ∠IJH=∠ICH/2=12°+x， ∠HIJ=(360°-∠JCH)/2=150°．
∠JIG=360°-∠HIJ-∠GIH=156°-x， ∠GBJ=∠GBC+∠CBJ=24°+xで， ∠JIG+∠GBJ=180°なので，四角形GBJIは円に内接し， ∠IGJ=∠IBJ=2x， ∠GJI=∠GBI=24°-x．
∠HGJ=∠HGI+∠IGJ=72°， ∠GJH=∠GJI+∠IJH=36°より， JG=JHであり， CH=CJ， ∠JCH=60°より△HJCは正三角形なので，JC=JH=JG．
∠GJC=∠GJH+∠HJC=96°なので， ∠JCG=42°．
∠JCB=∠JCG-30°=12°=18°-xより， x=6°．
∠DAB=60°-x=54°．

別解５

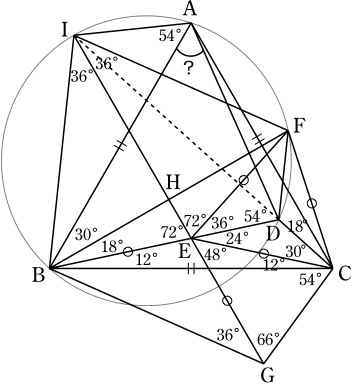∠BCD=42°．
線分BD上に ∠BCE=12°となるように点Eをとると，EB=EC， ∠DEC=24°， ∠ECD=30°．
正三角形FECを，直線CEから見てDと同じ側に作ると， ∠FED=36°．
線分BFの中点をHとすると，EB=EC=EFより，直線EHは線分BFの垂直二等分線で， BとFはEHを軸として互いに対称の位置にある．
∠BEH=∠HEF=72°， ∠FBE=18°， ∠FBC=30°．
ここで，直線EH上に，EG=EBとなる点Gを，Eから見てHと逆側にとると， ∠EBG=∠BGE=36°．
また，∠CEG=180°-∠HEF-∠FEC=48°， EG=EB=ECより， ∠EGC=∠GCE=66°で， ∠GCB=∠GCE-∠BCE=54°．
直線EH上に，HG=HIとなる点Iを，Hから見てGと逆側にとると， IとGはBFを軸として互いに対称の位置にあり， ∠ABF=30°=∠FBCより，AとCもBFを軸として互いに対称の位置にある．
BFについての対称性より，∠BAI=∠GCB=54°， ∠EIB=∠BGE=36°．
EHについての対称性より，∠FIE=∠EIB=36°．
∠EFI=180°-∠FIE-∠IEF=72°=∠IEFより，IE=IFであり， これとCE=CFより，EとFは直線CIを軸に互いに対称の位置にある．
∠ECI=∠ECF/2=30°=∠ECDより，点Dは直線CI上にあり， ∠BDI=∠DEC+∠ECD=54°=∠BAIなので，四角形IBDAは円に内接する．
∠DIE=∠FIE/2=18°より，∠DAB=∠DIB=∠DIE+∠EIB=54°．