証明

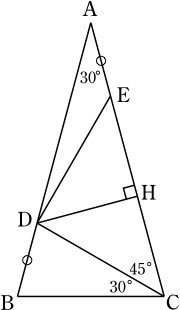AB=ACより， ∠ABC=∠BCA=75°．
∠CDB=75°=∠DBCより， DC=BC．
DからACに降ろした垂線の足をHとする．
∠DCH=45°より， CH=DH．
∠HAD=30°より， AD=2DH．
AE=BDより， EC=AC-AE=AB-BD=AD=2DH．
EH=EC-CH=2DH-DH=DH．
したがって， ∠HED=45°=∠DCHなので， DE=DC=BC．

別解（当初用意していた証明例）

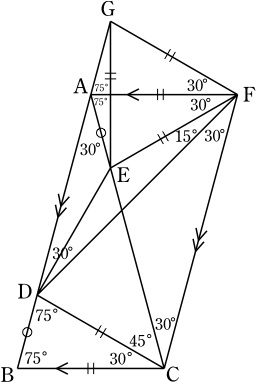∠ABC=∠BCA=75°， ∠CDB=∠DBC=75°より BC=DC， ∠DCA=45°．
Aを通りBCと平行な直線と，Cを通りABと平行な直線の交点をFとすると， ∠ACF=∠CAB=30°， ∠FAC=∠BCA=75°， ∠CFA=75°．
∠DCF=75°=∠BCA， FC=AC， DC=BCより， △FDC≡△ABC．
∴ ∠CFD=30°， ∠DFA=75°-30°=45°．
また， AE=BD， AF=BC， ∠FAE=∠DBC=75°より， △FAE≡△CBD， ∠AEF=75°， ∠EFA=30°．
ここで，直線AFに対しEと対称の位置に点Gをとると，対称性より， ∠GFA=∠EFA=30°， ∠AGF=∠AEF=75°， ∠FAG=∠FAE=75°， GF=EF．
∠FAG+∠FAC+∠CAB=75°+75°+30°=180°より，Gは直線AB上にある．
∠EFG=30°+30°=60°， GF=EFより， △GEFは正三角形．
∠DFG=30°+∠DFA=∠CFA， GF=EF=AF， DF=CFより， △DFG≡△CFAで， DG=DF， ∠GDF=30°．
対称性より，DEは∠GDFの二等分線であり， ∠EDF=15°．
∠EFD=75°-30°-30°=15°=∠EDFより， DE=EF=AF=BC．