答え　∠ACD=42°

証明

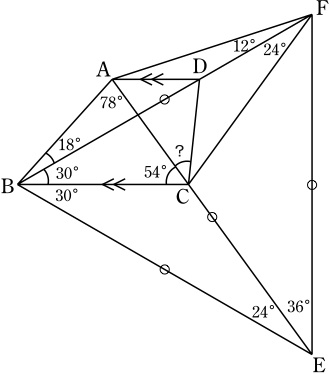∠CAB=78°， ∠BDA=30°， ∠DAC=54°．
直線AC上に， ∠ABE=∠CABとなるような点Eをとると， EA=EB， ∠BEA=24°， ∠DBE=60°， ∠CBE=30°．
半直線BD上に， ∠BEF=60°となるような点Fをとると， △BEFは正三角形となり， ∠FBC=∠CBE=30°なので， EとFは直線BCに対して対称の位置にあり， ∠CFB=∠BEC=24°．
また， ∠AEF=36°， EA=EB=EFより， ∠EFA=∠FAE=72°．
∠BFA=72°-60°=12°．
∠BFA＜∠BDAより，３点B，D，Fは直線BD上でこの順に並んでいる．
∠FAD=18°=∠ABFより， △FAD∽△FBA．
∴ FD:FA=FA:FB．
∠CFA=36°， ∠ACF=72°=∠FACより， FC=FA．
∴ FD:FC=FC:FB， △FCD∽△FBC．
∴ ∠DCF=∠FBC=30°．
∠ACD=72°-30°=42°．