証明

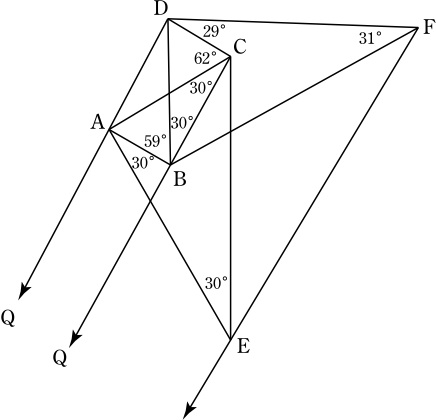直線ADと直線BCの交点をQとおく．

（四角形ABCDに着目）
∠CDB=58°， ∠CAB=61°．
ACとBDの交点をGとおくと， ∠GBC=∠BCG=30°より， GB=GC．
線分CD上に ∠CHG=62°となるように点Hをとると， ∠GCH=∠CHGより， GH=GC．
∠HGC=56°， ∠HGB=176°であり， GH=GC=GBなので， ∠GBH=∠BHG=2°．
ACとBHの交点をIとおくと， ∠HIC=∠HGI+∠IHG=58°=∠HDGとなり， ４点GIHDは同一円周上にある．
∴ ∠IDG=∠IHG=2°=∠GBI．
∴ ID=IB．
ここで，∠ABI=61°=∠IABより， IA=IB=IDであり， ∠DAI=∠IDAとなる．
∠DIC=∠DGI+∠IDG=62°より， ∠DAC=∠DAI=31°， ∠BDA=∠BGA-∠DAC=29°．
∠BCD+∠CDA=179°なので， 点QはAから見てDと逆側にあり， ∠DQC=1°．

（四角形AQECに着目）
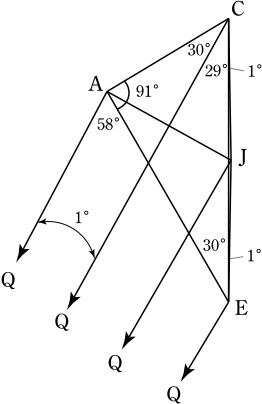∠CAB=61°， ∠CAE=91°， ∠ECQ=29°．
直線CQに対しAと対称の位置に点Jをとると， ∠QCA=30°より， △CAJは正三角形であり， ∠AEC=30°=∠AJC/2より，点Jは △CAEの外心となる．
∴ ∠CEJ=∠JCE=30°-29°=1°．
また，対称性より， ∠CQJ=∠AQC=1°=∠CEJとなり， ４点CQEJは同一円周上にある．
∴ ∠JQE=∠JCE=1°．
∠CQE=∠CQJ+∠JQE=2°．

（△DQFと点Bに着目）

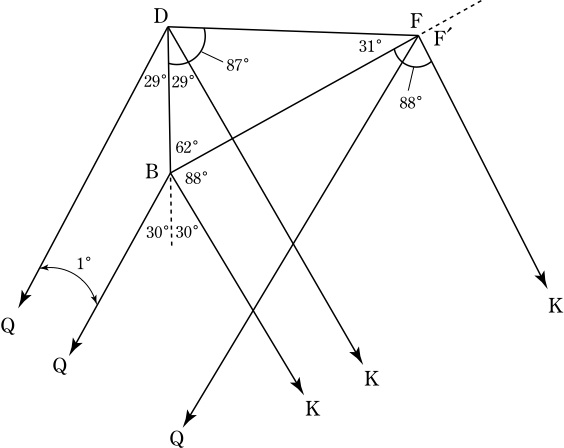
∠FDB=87°， ∠DBF=62°．
直線BDに対しQと対称の位置に点Kをとると， ∠QBD=150°より， △BQKは正三角形．
対称性より ∠BKD=∠DQB=1°， ∠KDB=∠BDQ=29°．
∠FBK=150°-62°＝88°．
半直線BF上に， ∠KF'B=88°となるように点F'をとると， KF'=KB=KQより，点Kは △BQF'の外心であり， ∠BKF'=4°より， ∠BQF'=2°， ∠QF'B=∠QKB/2=30°．
また， ∠DKF'=4°-1°=3°， ∠DQF'=2°+1°=3°=∠DKF'より， ４点DQKF'は同一円周上にあり， ∠QF'D=∠QKD=61°．
∠BF'D=∠QF'D-∠QF'B=31°=∠BFDなので，点F'と点Fは一致し， ∠BQF=∠BQF'=2°．

∠CQE=∠BQFより，３点FEQは同一直線上にある．
よって，３直線AD,BC,EFは１点で交わる．


※ http://www.gensu.co.jp/saito/langley/の系列でいうと，四角形ABCDでは系列1-17（x=31）の関係が，四角形AQECでは系列1-15（x=119）の関係が，△DQFと点Bでは系列1-16（x=31）の関係が成立しています．