月刊「理系への数学」幾何大王からの挑戦状
角度の問題
#17
解答例
→問題
答え
∠CAD=77°
証明
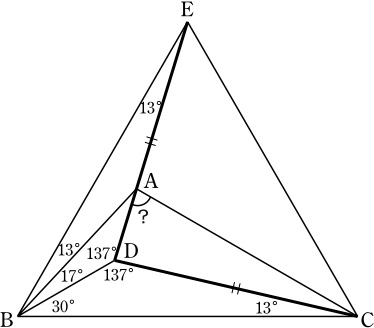∠DBC=180°-∠BCD-∠CDB=30°． 線分DAのA側の延長上に，DE=DCとなるように点Eをとると， ∠EDB=∠CDBより，二辺夾角相等で △DBE≡△DBCとなる． よって，BE=BC， ∠DBE=∠DBC=30°となり，△EBCは正三角形． また，∠BEA=∠BCD=13°， ∠EBA=∠DBE-∠ABD=13°=∠BEAなので， △AEBはAE=ABの二等辺三角形となり， 対称性より， ∠ACE=∠ACB=30°． ∠CEA=60°-∠BEA=47°， ∠CAD=∠CEA+∠ACE=77°．
∠DBC=180°-∠BCD-∠CDB=30°．
線分DAのA側の延長上に，DE=DCとなるように点Eをとると，
∠EDB=∠CDBより，二辺夾角相等で △DBE≡△DBCとなる．
よって，BE=BC， ∠DBE=∠DBC=30°となり，△EBCは正三角形．
また，∠BEA=∠BCD=13°， ∠EBA=∠DBE-∠ABD=13°=∠BEAなので，
△AEBはAE=ABの二等辺三角形となり，
対称性より， ∠ACE=∠ACB=30°．
∠CEA=60°-∠BEA=47°， ∠CAD=∠CEA+∠ACE=77°．