答え　∠DAE=30°

証明

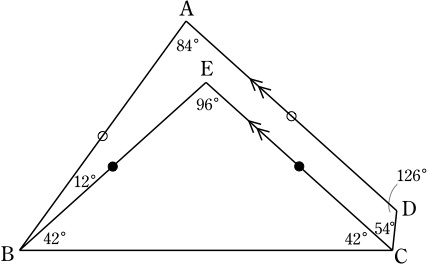EB=EC， ∠BEC=96°より， ∠EBC=∠BCE=42°．
AD//EC， ∠ECD=54°より， ∠CDA=126°．
∠DAB=360°-(12°+42°)-(42°+54°)-126°=84°．
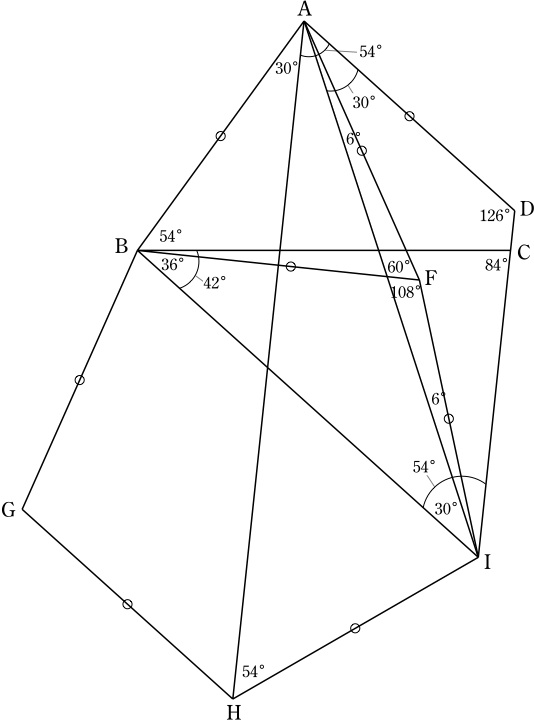ABを１辺とする正三角形ABFをABから見てEと同じ側に作り，BFを１辺とする正五角形BGHIFをBFから見てAと逆側に作る．
対称性より， ∠HAB=∠FAB/2=30°， ∠AHI=∠GHI/2=54°．
∠DAH=∠DAB-∠HAB=54=∠AHI， AD=AB=BF=HIより，
四角形AHIDは， AH//DI， AD=HIの等脚台形で，
∠IDA=180°-∠DAH=126°=∠CDA．
よって，点Cは直線ID上にある．
また， ∠FBI=∠BIF=36°，
∠CBI=∠ABI-∠ABC=(60°+36°)-(12°+42°)=42°，
∠ICB=180°-∠BCD=180°-(42°+54°)=84°,
∠BIC=180°-∠CBI-∠ICB=54°．
また， ∠IFA=60°+108°=168°， FA=FIより，
∠FAI=∠AIF=6°．
∠BIA=36°-6°=30°， ∠DAI=∠DAB-∠FAB+∠FAI=30°．
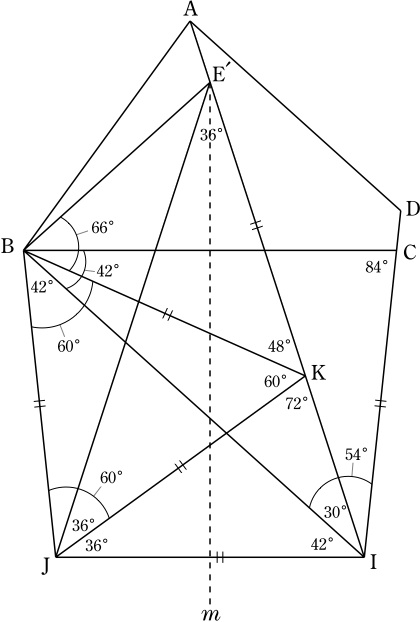BCの垂直二等分線を直線mとすると， B，Cはmを軸として互いに対称の位置にあり， EB=ECよりEはm上にある．
mを軸としてIと対称の位置にある点をJとすると，対称性より，
∠JBC=∠ICB=84°， BC//JI， ∠BJI=∠CIJ=96°．
∠IBJ=∠JBC-∠CBI=42°， ∠JIB=∠CIJ-∠BIC=42°=∠IBJより， BJ=JI．
∠JIA=∠JIB+∠BIA=72°．
半直線IA上に， ∠E'JI=∠JIAとなるように点E'をとると，
∠IE'J=36°で，E'はm上にある．
線分E'I上に ∠KJI=36°となるように点Kをとると，
∠IKJ=72°=∠JIKより，JK=JI=BJで，
∠BJK=∠BJI-∠KJI=60°なので， △BJKは正三角形．
また， ∠E'JK=36°=∠KE'Jより， E'K=JK=BK．
∠BKE'=180°-∠IKJ-∠JKB=48°， ∠E'BK=∠KE'B=66°．
∠E'BC=∠E'BK+∠KBJ-∠JBC=42°．
EもE'もm上にあり， ∠EBC=∠E'BCなので，EとE'は一致する．
∠DAE=∠DAE'=∠DAI=30°．