答え ∠EGF=40°
証明
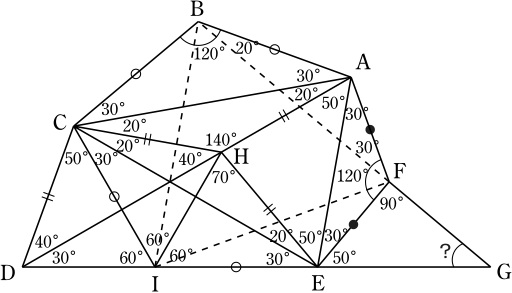 五角形ABCEFの内角の和より, ∠FAB=130°.
五角形ABCEFの内角の和より, ∠FAB=130°.
∠DAB=∠FAB-∠FAD=50°.
AB=BC, EF=FA, ∠ABC=∠EFA=120°より, ∠CAB=∠BCA=∠AEF=∠FAE=30°.
∠EAD=∠FAD-30°=50°, ∠DAC=∠DAB-30°=20°,
∠ACE=∠BCE-30°=40°, ∠CEA=∠CEF-30°=70°.
∠EAC=∠EAD+∠DAC=70°=∠CEAより, CA=CE.
∠CDA=180°-∠DAC-∠ACD=180°-20°-(40°+80°)=40°.
△ACEの外心をHとおくと, HA=HC=HE.
∠EHC=2∠EAC=140°, ∠HCE=∠CEH=20°.
∠CHA=2∠CEA=140°, ∠HAC=∠ACH=20°.
∠HAC=∠DACより,HはAD上にあり,
∠DHC=∠HAC+∠ACH=40°=∠CDAより, DC=HC, ∠HCD=100°.
∠HCDの二等分線と∠EHCの二等分線の交点をIとすると,
△CDI≡△CHI(二辺夾角相等), △CHI≡△EHI(二辺夾角相等)が言え,
∠CDI=∠CHI=∠EHC/2=70°, ∠ICD=∠HCD/2=50°,
∠DIC=180°-∠CDI-∠ICD=60°.
∠DIC+∠HIC+∠HIE=3∠DIC=180°より,IはDE上にあり,
∠DEC=∠IEH-∠CEH=∠ICD-∠CEH=30°.
∠FEG=180°-∠DEC-∠CEF=50°.
IE=ICより, ∠ECI=∠IEC=30°=∠BCA=∠CABであり,
CA=CEなので, △BCA≡△ICE, BC=IC.
∠BCI=∠BCE+∠ECI=100°より, ∠CIB=∠IBC=40°.
ここで, △ACEにおいて,ナポレオンの定理より
△BIFは正三角形で, ∠FBI=60°.
∠ABF=∠ABC-∠IBC-∠FBI=20°,
∠BFA=180°-∠FAB-∠ABF=30°,
∠EFB=∠EFA-∠BFA=90°,
∠EGF=∠EFB-∠FEG=40°.
|