問題（ラングレーの問題）

凸四角形ABCDにおいて， ∠ABD=20°， ∠DBC=60°， ∠BCA=50°， ∠ACD=30°のとき， ∠BDAを求め，その角度となることを初等幾何で証明してください．

答え　∠BDA=30°

証明例1（系列1-13としての証明）

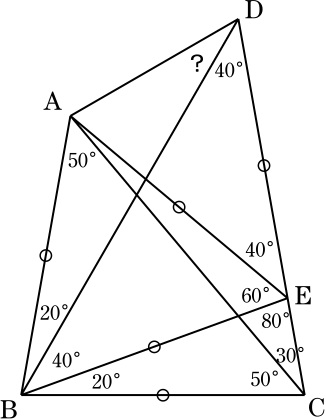
線分DC上に ∠EBC=20°となるように点Eをとると， ∠BCE=∠CEB=80°より， BC=BE．
∠BCA=∠BAC=50°より， BC=BA．
よって， BA=BEとなり， ∠ABE=60°より △ABEは正三角形．
∠DBE=∠EDB=40°なので， DE=BE=AE．
したがって，３点A,B,DはEを中心とする同一円周上にあり，円周角の定理より， ∠BDA=∠BEA/2=30°．

証明例2（系列1-13としての証明）

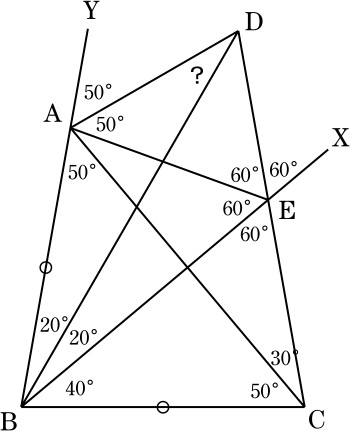∠ABCの二等分線と線分CDとの交点をEとし， 線分BEのE側の延長上に点Xを，線分ABのA側の延長上に点Yをそれぞれとる．
∠CAB=50°=∠BCAなので， BC=BAであり， ２点A,Cは， ∠ABCの二等分線である直線BEを軸に互いに対称の位置にある．
∠CEB=60°なので，対称性より ∠BEA=60°であり， ∠AED=∠DEX=60°となるので，直線DEは ∠AEXの二等分線．
また， ∠ABE=∠ABC/2=40°=2∠ABDより，直線BDは ∠ABEの二等分線．
よって，点Dは △ABEの ∠ABEの内側にある傍心となり， 直線ADは ∠YAEの二等分線である．
∠YAE=∠ABE+∠BEA=100°， ∠YAD=∠YAE/2=50°，
∠BDA=∠YAD-∠ABD=30°．

証明例3（系列1-13としての証明）

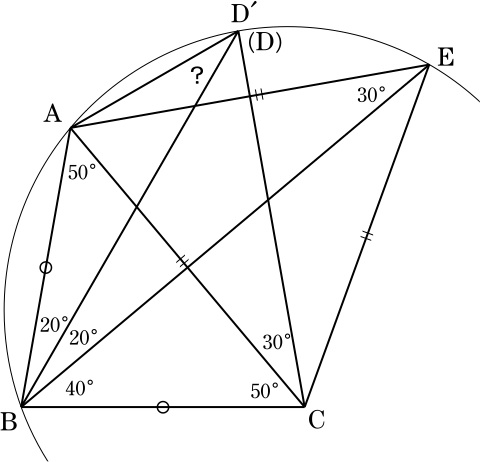ACを１辺とする正三角形ACEをACから見てBと逆側に作る．
∠BCA=∠CAB=50°より， BC=BAなので，四角形ABCEはBEを対称軸とする凧型となり， ∠ABE=∠ABC/2=40°， ∠BEA=∠CEA/2=30°．
また， ∠ACD=30°より，直線CDは線分AEの垂直二等分線となる．
ここで， △ABEの外接円の劣弧AEと直線CDとの交点をD'とすると， 対称性より， 弧AD'=弧D'Eとなり， 円周角の定理より， ∠ABD'=∠D'BE=∠ABE/2=20°=∠ABD．
よって，D'はDと一致し，円周角の定理より ∠BDA=∠BEA=30°．

証明例4（系列1-5としての証明）

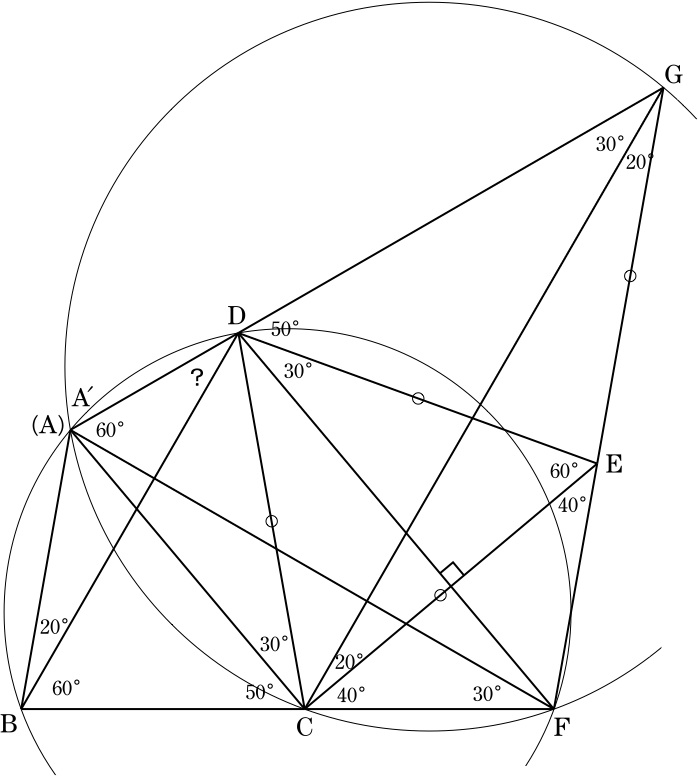CDを一辺とする正三角形DCEをCDから見てBと逆側に作り，DからAEに降ろした垂線と直線BCとの交点をFとする．また，線分FEのE側の延長上にEG=ECとなるような点Gをとり，△GCFの外接円と直線DGとの点G以外の交点をA'とする．
対称性より， ∠FEC=∠ECF=180°-50°-30°-60°=40°．
EG=ECより， ∠EGC=∠GCE=∠FEC/2=20°．
EG=EC=EDより， ∠EGD=∠GDE=∠FED/2=(60°+40°)/2=50°．
４点A'CFGが同一円周上にあるので， ∠BCA'=∠FGA'=50°， ∠GA'F=∠GCF=20°+40°=60°．
∠DA'F=60°=∠DBFより，４点A'BFDは同一円周上にあり， ∠A'BF=∠GDF=50°+30°=80°．
∠BCA'=50°=∠BCA， ∠A'BC=∠ABC=80°より， A'はAと一致する．
∠CGA=∠EGD-∠EGC=30°， ∠BFA=∠CFA=∠CGA=30°（４点ACFGは同一円周上）．
∠BDA=∠BFA=30°（４点ABFDは同一円周上）．

証明例5（The Mathematical Gazette誌で最初に紹介された証明の１つ）

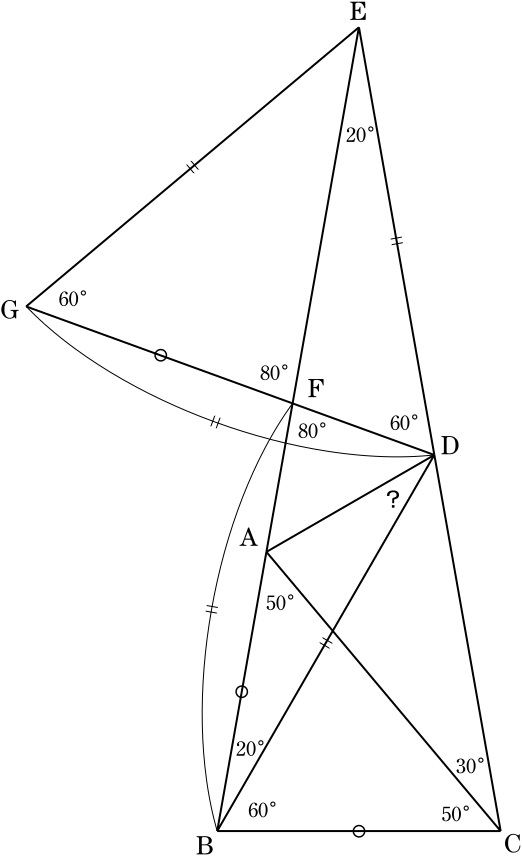直線ABと直線DCの交点をEとすると， ∠ABC=∠BCD=80°よりEB=EC， ∠CEB=20°=∠ABDより BD=ED．
∠CAB=50°=∠BCAより，BA=BC．
線分EB上にBF=BDとなるように点Fをとり，線分DFのF側の延長上にFG=BCとなるように点Gをとる．
∠DFB=∠BDF=80°より， ∠GDE=∠DFB-∠DEF=60°．
∠GFE=80°=∠BCD， EF=EB-BF=EB-BD=EC-ED=DCより， △EGF≡△DBC（二辺夾角相等）で， ∠EGD=∠DBC=60°．
よって，△EGDは正三角形．
FA=BF-BA=BD-BC=ED-FG=GD-FG=FD．
∴ ∠ADF=∠FAD=50°， ∠BDA=∠BDF-∠ADF=30°．

証明例6（The Mathematical Gazette誌で最初に紹介された証明の１つ）

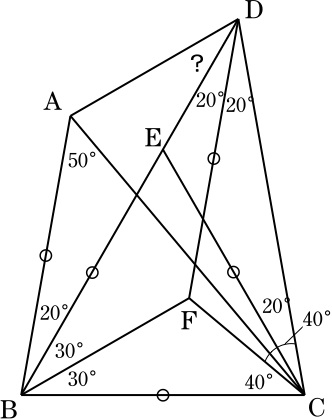線分BD上にBE=BCとなるように点Eをとり， △DBCの内心をFとする．
∠EBC=60°より， △EBCは正三角形．
∠DBF=∠FBC=30°， ∠BCF=∠FCD=40°， ∠CDF=∠FDB=20°．
∠DCE=20°=∠CDF， ∠EDC=40°=∠FCDより， △EDC≡△FCD．
∴ FD=EC=BC=BA （∵ ∠CAB=50°=∠BCA）．
また， ∠FDB=20°=∠ABDより， FD//BA．
よって，四角形ABFDは平行四辺形で， ∠BDA=∠DBF=30°．

証明例7（The Mathematical Gazette誌で最初に紹介された証明の１つ）

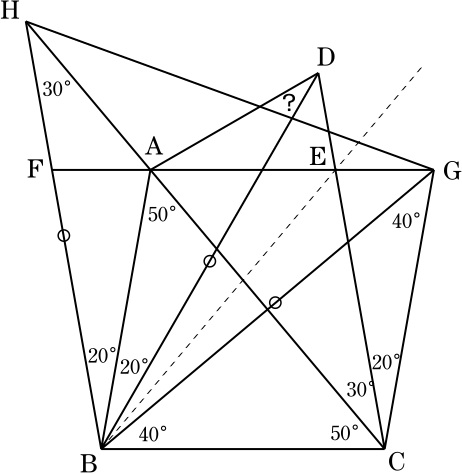Aを通る直線BCの平行線と線分CDの交点をEとし，Bを通る直線CDの平行線と直線AEの交点をF，Cを通る直線BAの平行線と直線AEの交点をG，直線BFと直線CAの交点をHとする．
∠CAB=50°=∠BCAより，平行四辺形ABCGは菱形．
∠ABC=∠BCE=80°より，台形ABCEはAB=ECの等脚台形．
平行四辺形ECBF≡平行四辺形ABCGとなるので，四角形FBCEも菱形．
∠GBC=∠ABG=40°， ∠FBC=180°-∠BCE=100°より， ∠FBG=60°=∠CBD．
ここで，菱形の対称性より，直線BEを軸として線分BFと線分BCは互いに対称なので，直線BGと直線BDも互いに対称であり，また，直線FEと直線CEも互いに対称なので，２点G,Dは直線BEを軸に対称の位置にある．
よって， BG=BD．
さらに，直線CAを軸とした対称性より， ∠HGB=∠HBG=60°で， △HBGは正三角形．
BH=BG=BD， ∠ABH=20°=∠ABDより， △HBA≡△DBAであり， ∠BDA=∠BHA=30°．

証明例8（「フランクリンの凧」という通称の元となった証明）

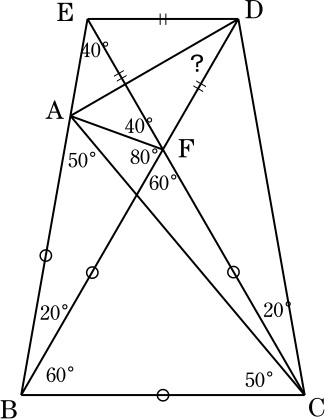Dを通る直線BCの平行線と直線BAの交点をEとし，線分BDと線分CEの交点をFとする．
∠EBC=∠BCD=80°より，台形EBCDは EB=DCの等脚台形で， ∠BCE=∠DBC=60°となるので， △FBCと△FDEはともに正三角形．
また， ∠CAB=50°=∠BCAより， BA=BC=BFなので， ∠BFA=∠FAB=80°．
∠FEA=40°， ∠AFE=180°-∠CFB-∠BFA=40°=∠FEAより， AE=AF．
よって，四角形EAFDはADを対称軸とする凧型であり， ∠BDA=∠FDE/2=30°．

証明例9（mathcircle.berkeley.eduより）

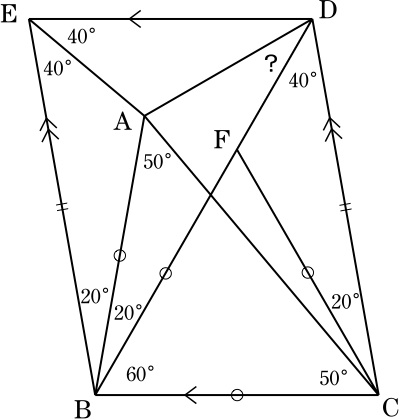BC，CDを２辺とする平行四辺形EBCDを作り，線分BD上に BF=BCとなるような点Fをとる．
∠FBC=60°なので， △FBCは正三角形．
∠FCD=∠BCD-60°=20°．
∠EBA=∠EBC-∠ABC=100°-80°=20°．
∠CAB=50°=∠BCAより， BA=BC=CF．
EB=DC， ∠EBA=∠FCDなので， △EBA≡△DCF（二辺夾角相等）．
よって， ∠AEB=∠CDF=40°．
∠DEB=∠BCD=80°より， ∠DEA=40°=∠AEBであり， ∠EBA=∠ABD（=20°）なので， 点Aは△EBDの内心．
∠BDE=∠DBC=60°より， ∠BDA=∠BDE/2=30°．

証明例10（mathcircle.berkeley.eduより）

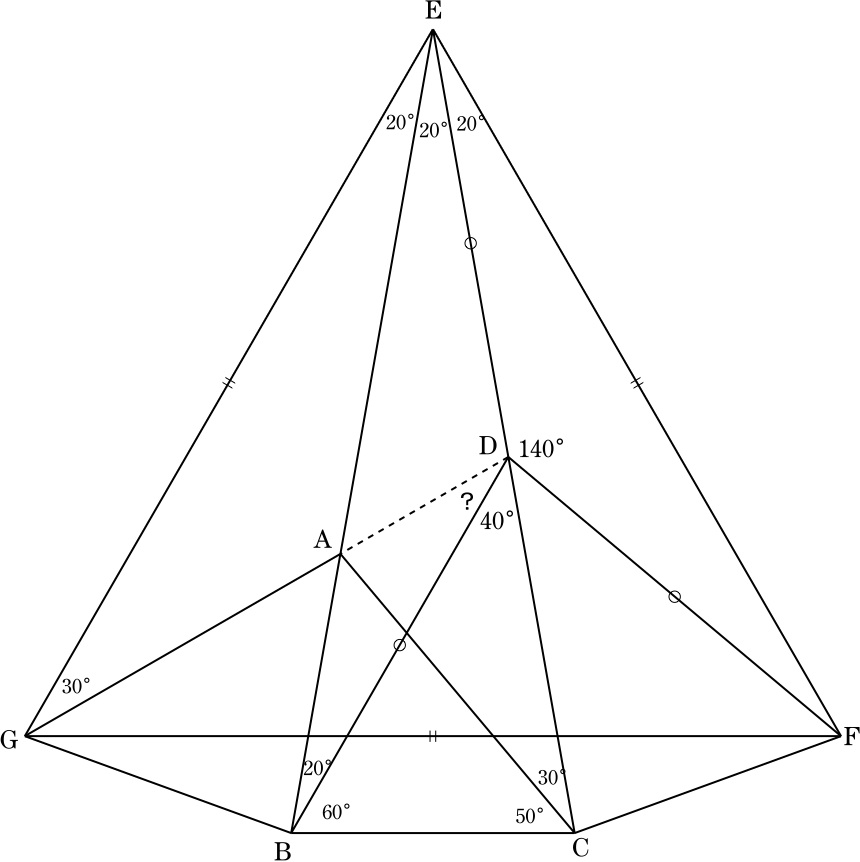直線ABと直線DCの交点をEとすると，∠ABC=∠BCD=80°よりEB=EC， ∠CEB=20°=∠ABDより DB=DE．
直線ECを軸に点Bと対称の位置に点Fをとると，対称性より EF=EB， DF=DB=DE， ∠EDF=∠BDE=140°， ∠FEC=∠CEB=20°．
直線EBを軸に点Cと対称の位置に点Gをとると，対称性より EG=EC， ∠EGA=∠ACE=30°， ∠BEG=∠CEB=20°．
EG=EC=EB=EF， ∠FEG=20°+20°+20°=60°より， △EGFは正三角形．
∠EGA=30°より，直線GAは線分EFの垂直二等分線であり， DF=DEより，点Dは線分EFの垂直二等分線上にあるので， ３点GADは同一直線上にある．
直線GAについての対称性より， ∠GDE=∠FDG=(360°-∠EDF)/2=110°．
∠BDA=180°-∠CDB-∠GDE=180°-40°-110°=30°．

証明例11（jwilson.coe.uga.eduより）

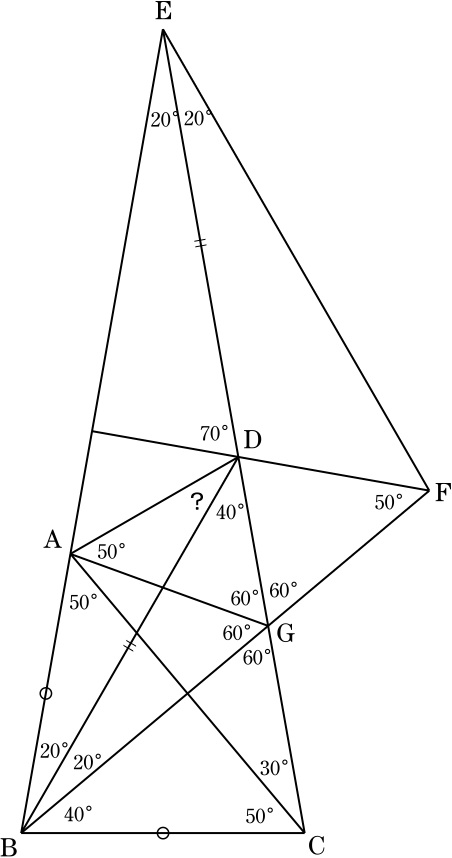直線ABと直線DCの交点をEとすると， ∠CEB=20°=∠ABDより DB=DE．
また， ∠CAB=50°=∠BCAより， BA=BC．
∠ABCの二等分線と∠BDEの二等分線の交点をFとし，BFとDCの交点をGとする．
BA=BCより，２点A,Cは直線BFを軸に互いに対称の位置にある．
また，DE=DBより，２点E,Bは直線DFを軸に互いに対称の位置にある．
∠ABG=∠GBC=∠ABC/2=40°， ∠DBF=∠ABG-∠ABD=20°， ∠FED=∠DBF=20°．
∠BGA=∠CGB=60°， ∠AGE=180°-60°-60°=60°， ∠EGF=∠CGB=60°．
∠FEG=∠GEA， ∠EGF=∠AGEより， △EAG≡△EFG（二角夾辺相等）なので， ２点A,Fは直線EGを軸に互いに対称の位置にある．
∠BFD=90°-∠EBF=50°， ∠DAG=∠GFD=50°．
∠GDA=180°-∠DAG-∠AGE=70°，
∠BDA=∠GDA-∠CDB=70°-40°=30°．

証明例12（「技術系サラリーマンの交差点」より）

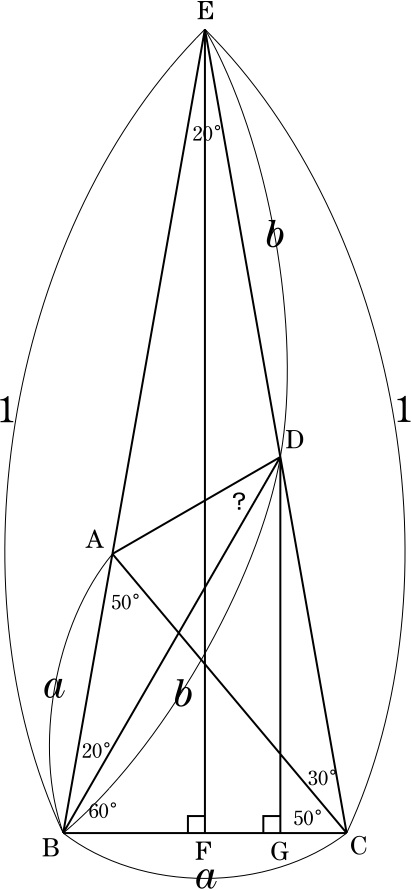直線ABと直線DCの交点をEとすると， ∠ABC=∠BCD=80°より EB=EC， ∠CEB=20°=∠ABDより DB=DE．
また，∠CAB=50°=∠BCAより， BA=BC．
EからBCに降ろした垂線の足をF，DからBCに降ろした垂線の足をGとする．
ここで， EB=EC=1として， BA=BC=a， DB=DE=bとおく．
EB=ECより， BF=FC=a/2．
∠DBC=60°より， BG=DB/2=b/2， FG=BG-BF=(b-a)/2．
また， FG:FC=ED:EC=b:1より， FG=b・FC=ab/2．
よって， (b-a)/2=ab/2となり， b=a/(1-a)．
BA:BD=a:b=a:a/(1-a)=1-a:1=EA:ECであり， ∠ABD=∠AEC（=20°）なので， △ABD∽△AEC．
∴ ∠BDA=∠ECA=30°．

正弦定理を用いた証明

∠BDA = θとおく．
∠DAB = 160° - θ， ∠BCD = 80°， ∠CDB = 40°なので，
正弦定理より，
AB/sinθ = BD/sin(160°-θ) = BD/sin(20°+θ)，
BC/sin40° = BD/sin80°．
∠CAB=50° = ∠BCAより， AB = BCなので，
sinθ/sin(20°+θ) = sin40°/sin80°．
sinθ・sin80° = sin(20°+θ)・sin40°
= (sin20°・cosθ + cos20°・sinθ)sin40°
= sin20°・sin40°・cosθ + cos20°・sin40°・sinθ．
tanθ = sinθ / cosθ
= sin20°・sin40° / (sin80° - cos20°・sin40°)
= sin20°・sin40° / (2sin40°・cos40° - cos20°・sin40°)
= sin20° / (2cos40° - cos20°)．
ここで，
sin20° = sin(60°-40°)
= (√3/2)cos40° - (1/2)sin40°，
cos20° = cos(60°-40°)
= (1/2)cos40° + (√3/2)sin40°，
2cos40° - cos20°
= (3/2)cos40° - (√3/2)sin40°
= √3sin20°
なので，
tanθ = sin20°/(√3sin20°) = 1/√3．
∴ ∠BDA = θ = 30°．

チェバの定理の代数的な言い換えを用いた証明

△DBCの外接円と直線CAとのC以外の交点をEとおく．
円周角の定理より， ∠BDE=∠BCA=50°， ∠DEC=∠DBC=60°， ∠CEB=∠CDB=40°， ∠EBD=∠ACD=30°， ∠EBA=∠EBD-∠ABD=10°．
BE上に， ∠BDF=30°となる点Fをとると， ∠FDE=20°．
チェバの定理の逆の三角関数表現より，△EBDにおいて，
sin∠BDF・sin∠DEA・sin∠EBA = sin∠FDE・sin∠AEB・sin∠ABD
が成り立つならば，３直線DF，EA，BAは１点で交わる．
S = sin∠BDF・sin∠DEA・sin∠EBA-sin∠FDE・sin∠AEB・sin∠ABD
= sin30°・sin60°・sin10°-sin20°・sin40°・sin20°とおく．
ここで，sinθ = (e^(iθ)-e^(-iθ))/(2i)と表されるので，
ω = e^(2iπ/3) とおき，
e^(iπ) = -1， 1+ω+ω^2 = 0を用いると，
((2i)^3)S
= (e^(iπ/6)-e^(-iπ/6))(e^(iπ/3)-e^(-iπ/3))(e^(iπ/18)-e^(-iπ/18))
　-(e^(iπ/9)-e^(-iπ/9))^2(e^(2iπ/9)-e^(-2iπ/9))
= e^(5iπ/9)-e^(4iπ/9)-e^(-iπ/9)+e^(-2iπ/9)
　-e^(2iπ/9)+e^(iπ/9)+e^(-4iπ/9)-e^(-5iπ/9)
　-e^(4iπ/9)+1+2e^(2iπ/9)-2e^(-2iπ/9)-1+e^(-4iπ/9)
= e^(5iπ/9)-e^(4iπ/9)-e^(-iπ/9)-e^(-2iπ/9)
　+e^(2iπ/9)+e^(iπ/9)+e^(-4iπ/9)-e^(-5iπ/9)
　-e^(4iπ/9)+e^(-4iπ/9)
= e^(5iπ/9)+e^(13iπ/9)+e^(8iπ/9)+e^(7iπ/9)
　+e^(2iπ/9)+e^(iπ/9)+e^(14iπ/9)+e^(4iπ/9)
　-e^(4iπ/9)-e^(5iπ/9)
= e^(iπ/9)+e^(7iπ/9)+e^(13iπ/9)
　+e^(2iπ/9)+e^(8iπ/9)+e^(14iπ/9)
= e^(iπ/9)(1+ω+ω^2)+e^(2iπ/9)(1+ω+ω^2)
= 0．
よって，S=0より
sin∠BDF・sin∠DEA・sin∠EBA = sin∠FDE・sin∠AEB・sin∠ABD
が成り立ち，３直線DF，EA，BAは１点で交わる．
すなわち，点Aは直線DF上にあり，
∠BDA = ∠BDF = 30°．