答え ∠ARF=5°, ∠RQP=3°, ∠QPR=1°
証明
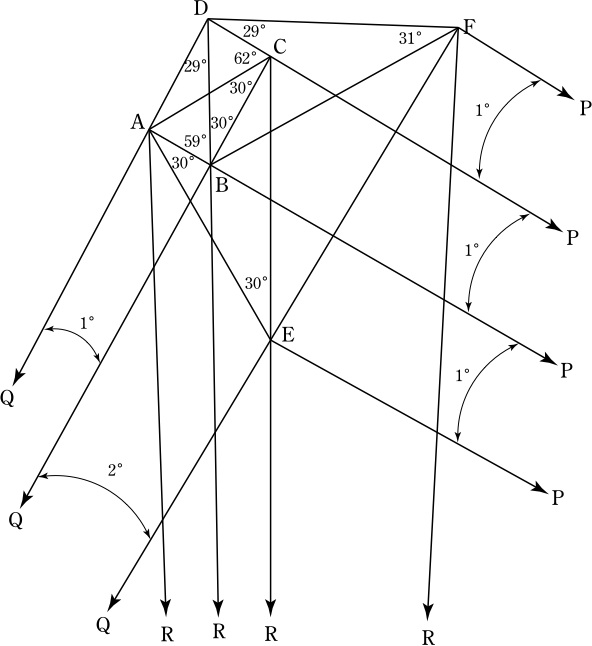
 ∠ECB=29°, ∠CDB=58°より, ∠ECD+∠CDB=179°となるので,
点RはCからみてEと同じ側にあり, ∠DRC=1°.
∠ECB=29°, ∠CDB=58°より, ∠ECD+∠CDB=179°となるので,
点RはCからみてEと同じ側にあり, ∠DRC=1°.
∠DRC=∠DQCより,4点DQRCは同一円周上にあり,
∠DQR=180°-∠RCD=59°, ∠QRD=∠QCD=92°.
∠DAB=92°=∠QRBより,4点AQRBは同一円周上にあり,
∠ARB=∠AQB=1°.
∠BRC=∠BPC(=1°)より,4点BRPCは同一円周上にあり,
∠RPB=∠RCB=29°, ∠RPC=29°+1°=30°, ∠RPF=30°+1°=31°.
∠DAE=122°, ∠DQF=3°より, ∠EAQ=58°, ∠AEF=61°, ∠CEF=31°.
∠RPF=∠CEFより,4点ERPFは同一円周上にあり,
∠ERF=∠EPF=1°+1°+1°=3°.
∠ARF=∠ARB+∠DRC+∠ERF=5°.
∠AQC=∠APC(=1°)より,4点AQPCは同一円周上にあり,
∠AQP=∠ACD=62°, ∠QPC=∠DAC=31°.
∠RQP=∠AQP-∠DQR=3°, ∠QPR=∠QPC-∠RPC=1°.
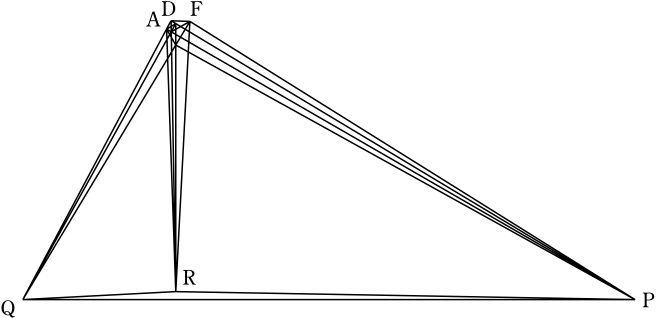
※ #7〜#9で与えられたA〜Fの6点はそれぞれ独立に,PQRの3点と組み合わせた4点で整角三角形を形成しています.http://www.gensu.co.jp/saito/langley/の1変数系列の中に,これら6つの整角三角形が見つかるはずです.
|