答え ∠EHG=71°
証明
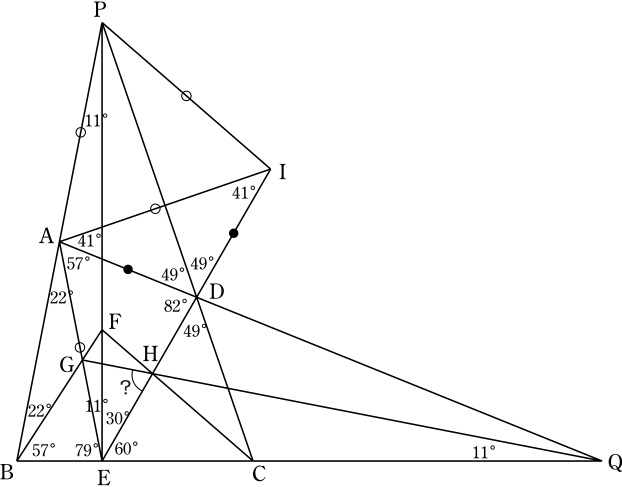 ∠AED=180°-∠BEA-∠DEC=41°,
∠AED=180°-∠BEA-∠DEC=41°,
∠AEF=∠AED-∠FED=11°,
∠DAE=180°-∠AED-∠EDA=57°,
∠DAB=∠DAE+∠EAB=79°.
直線BAと直線EFの交点をPとすると,
∠EPA=∠EAB-∠AEF=11°=∠AEPなので, AE=AP.
APを1辺とする正三角形PAIを,IがPAから見てCと同じ側にあるように作ると,
∠IAE=180°-∠PAI-∠EAB=98°, AI=AP=AEより,
∠EIA=∠AEI=41°=∠AED.
よって,3点E,D,Iは同一直線上にあり, ∠DIA=41°.
∠ADI=180°-∠EDA=98°.
∠IAD=∠EDA-∠DIA=41°=∠DIAより, DI=DAとなり,
△ADP≡△IDP(三辺相等).
∴ ∠ADP=∠PDI=∠ADI/2=49°.
∠CDE+∠EDA+∠ADP=180°より,3点P,D,Cは同一直線上にある.
∠ABC=180°-∠BEA-∠EAB=79°, ∠ABF=∠ABC-∠FBE=22°.
直線ADと直線BCの交点をQとすると,
∠GAB=∠ABG=22°, ∠QAB=∠ABQ=79°より,
G,Pはいずれも線分ABの垂直二等分線上にあり,
∠BQG=90°-∠ABQ=11°.
ここで,直線AB,EF,DCが1点Pで交わっているので,
デザルグの定理より,
AEとBFの交点G,EDとFCの交点H,ADとBCの交点Qは同一直線上にある.
∴ ∠EHG=∠HEQ+∠EQH=60°+11°=71°.
※なお,アフィン平面におけるデザルグの定理は,メネラウスの定理で証明できるので,上記証明の「デザルグの定理より」以降を次のようにメネラウスの定理で置き換えることができる.
メネラウスの定理より,
△PBCと直線AQについて (CQ/QB)・(BA/AP)・(PD/DC)=1
△PBFと直線AEについて (BG/GF)・(FE/EP)・(PA/AB)=1
△PFCと直線EDについて (FH/HC)・(CD/DP)・(PE/EF)=1
3式の左辺を掛けると,(CQ/QB)・(BG/GF)・(FH/HC)=1となり,
△BCFについて,メネラウスの定理の逆より,
3点Q,G,Hは同一直線上にある.
(以下同じ)
|