答え

(1)　∠DBC= [1] 48°　[2] 24°　[3] 66°

(2)　∠BDA= [1] 12°　[2] 18°　[3] 6°

証明

[1]　∠DBC=48°の場合

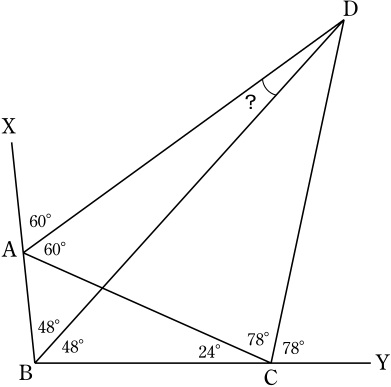線分ABのA側の延長上に点X，線分BCのC側の延長上に点Yを取る．
∠XAC=∠ABD+∠DBC+∠BCA=120°．
∠DCY=180°-∠BCA-∠ACD=78°=∠ACD， ∠ABD=∠DBCより，点Dは △ABCの ∠Bの内側にある傍心．
∴ ∠XAD=∠XAC/2=60°．
∠BDA=∠XAD-∠ABD=12°．

[2]　∠DBC=24°の場合

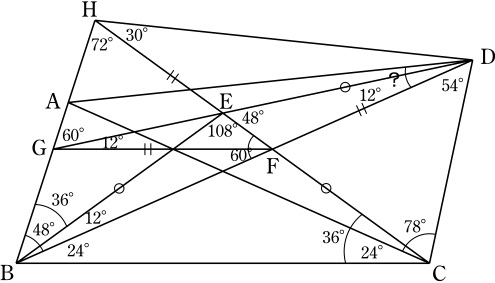∠CDB=180°-∠DBC-(∠BCA+∠ACD)=54°．
△BCDの外心をEとすると， ∠CEB=2∠CDB=108°， ∠DEC=2∠DBC=48°， ∠DEB=∠DEC+∠CEB=156°．
∠EBC=∠BCE=(180°-∠CEB)/2=36°， ∠EBD=∠BDE=(180°-∠DEB)/2=12°．
∠ABE=∠ABD-∠EBD=36°．
BDとCEの交点をFとし，直線BAと直線DEの交点をG，直線BAと直線CEの交点をHとする．
∠BFE=∠DBC+∠BCE=60°， ∠HGE=∠BDE+∠ABD=60°より，四角形GBFEは円に内接する．
よって， ∠DGF=∠EBF=12°=∠BDE=∠FDGとなり， FD=FG．
また， ∠FHG=180°-(∠ABD+∠DBC)-∠BCE=72°， ∠HGF=∠HGE+∠DGF=72°=∠FHGより， FH=FG．
FD=FG=FHより， ∠FDH=∠DHF=∠BFE/2=30°．
∠DHA=∠DHF+∠FHG=102°．
∠DHA+∠ACD=180°より，四角形HACDは円に内接するので， ∠CDA=∠CHA=∠FHG=72°．
∠BDA=∠CDA-∠CDB=18°．

[3]　∠DBC=66°の場合

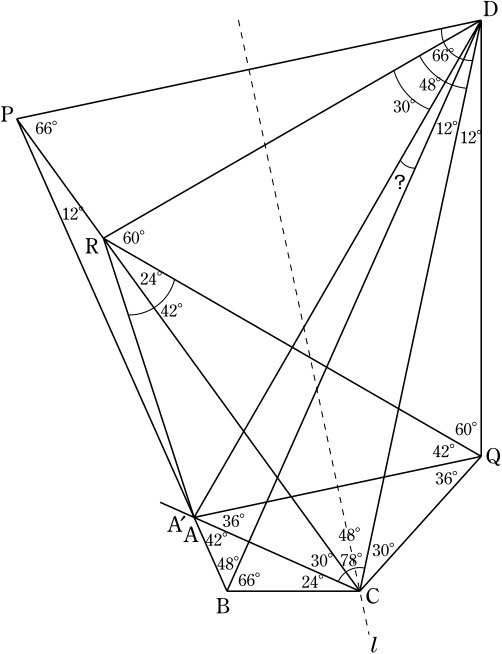∠CDB=180°-∠DBC-(∠BCA+∠ACD)=12°， ∠CAB=180°-(∠ABD+∠DBC)-∠BCA=42°．
線分ABのA側の延長上に， ∠CPB=12°となるように点Pを取ると， ∠PAC=180°-∠CAB=138°， ∠ACP=∠CAB-∠CPB=30°．
∠CPB=∠CDBより4点P,B,C,Dは同一円周上にあり， ∠DPC=∠DBC=66°．
∠PCD=∠ACD-∠ACP=48°，
∠CDP=180°-∠DPC-∠PCD=66°=∠DPCなので， CD=CP．
∠PCDの二等分線をmとすると，PとDはmを軸として互いに対称の位置にある．
mを軸として，Aと対称の位置に点Qを取ると，対称性より， △QDC≡△APCとなり， ∠DCQ=∠ACP=30°， ∠CQD=∠PAC=138°， ∠QDC=∠CPA=12°， ∠PCQ=∠PCD+∠DCQ=78°．
また，CQ=CA， ∠ACQ=∠ACD+∠DCQ=108°より， ∠CQA=∠QAC=36°， ∠AQR=∠CQR-∠CQA=42°．
線分PC上に， ∠QRC=24°となるように点Rを取ると， ∠CQR=180°-∠QRC-∠PCQ=78°=∠PCQよりRC=RQ．
∠RQD=∠CQD-∠CQR=60°．
ここで， ∠QDC=∠QRC/2より，３点C,Q,DはRを中心とする同一円周上にある．
よって， ∠DRQ=2∠DCQ=60°となり， △DRQは正三角形．
RC=RQ=RDより， ∠CDR=∠PCD=48°．
∠QDRの二等分線と直線CAの交点をA'とすると， ∠A'DR=30°=∠ACR=∠A'CRより， ４点D,R,A',Cは同一円周上にある．
∠A'CD=∠ACD=78°， ∠DRA'=180°-∠A'CD=102°， ∠QRA'=∠DRA'-∠DRQ=42°．
２点Q,Rは直線DA'を軸に互いに対称なので， ∠A'QR=∠QRA'=42°=∠AQR．
よって，点A'は直線QA上にあり，点AとA'はともにQAとCAの交点となるので，一致する．
∠BDA=∠CDR-∠CDB-∠A'DR=6°．