証明

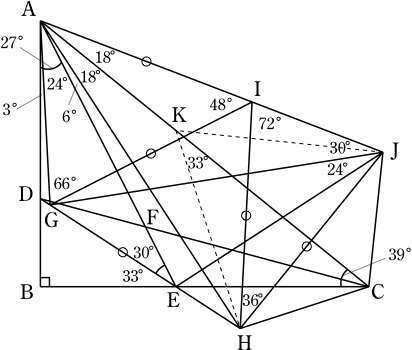∠CAB=51°， ∠CAF=24°， ∠EDB=57°， ∠BED=33°．
線分DE上に ∠GAD=3°となるように点Gをとり，線分DEのE側の延長上に ∠HAE=6°となるように点Hをとる．
さらに，GHを１辺とする正三角形GHIを，直線DEからみてAと同じ側に作り，線分AIのI側の延長上に ∠IHJ=36°となるように点Jをとる．
∠EAG=27°-3°=24°， ∠HAG=24°+6°=30°， ∠CAH=24°-6°=18°．
∠HAG=30°より，３点A,G,HはIを中心とする円周上にあり，AI=GI．
∠DGA=∠EDB-∠GAD=54°より， ∠AGI=66°であり，
AI=GIより， ∠IAG=66°， ∠GIA=48°．
∠JIH=72°， ∠IHJ=36°より， ∠HJI=72°， HJ=HI．
HJ=HI=HGより， ∠GJI=30°．
∠GJA=∠GJI=30°=∠DEA=∠GEAより，４点AGEJは同一円周上にあり，
∠JEH=∠JAG=∠IAG=66°．
∠CEH=∠BED=33°なので， ∠JEC=66°-33°=33°．
∠JAH=∠IAG-∠HAG=36°， ∠HJA=72°より， ∠AHJ=72°で，AJ=AH．
∠JAC=18°=∠CAHより，ACは∠JAHの二等分線であり，
2点J,Hは直線ACに対し互いに対称の位置にある．
線分AC上に， ∠JKH=66°となるように点Kをとると，
∠JEH=∠JKHより，４点KEHJは同一円周上にあり，
さらに ∠CKH=33°=∠CEHより，４点KEHCは同一円周上にあるので，
結局５点KEHCJは同一円周上にあることになり，
∠HCJ=180°-66°=114°， ∠HCA=57°．
∠HDB=57°=∠HCAより，４点ADHCは同一円周上にあり，
∠FCA=∠DCA=∠DHA=30°-6°=24°， ∠FCA=∠CAFより，AF=FC．