代数的証明
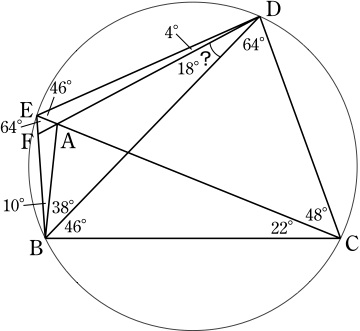∠CDB=180°-∠DBC-(∠BCA+∠ACD)=64°．
線分ACのA側の延長上に， ∠EBA=10°となるように点Eを取ると， ∠EBD=48°=∠ACD=∠ECDより，４点E,B,C,Dは同一円周上にある．
円周角の定理より， ∠CEB=∠CDB=64°， ∠DEC=∠DBC=46°， ∠BDE=∠BCE=22°．
ここで，線分EB上に ∠BDF=18°，すなわち， ∠FDE=4°となるように点Fを取り，
S=sin∠DEC・sin∠EBA・sin∠BDF-sin∠CEB・sin∠ABD・sin∠FDE
=sin46°・sin10°・sin18°-sin64°・sin38°・sin4°とおく．
オイラーの公式より， e^(iπx/180)=cosx°+i・sinx°となるので，
ζ=e^(iπ/180)とおくと， 2i・sinx°=ζ^x-ζ^(-x)と表せる．
さらに， ζ^180=-1， ζ^360=1であり，
ω=ζ^120， ξ=ζ^72とおくと， 1+ω+ω^2=0， 1+ξ+ξ^2+ξ^3+ξ^4=0．
これらを使うと，
(2i)^3・S
=(ζ^46-ζ^(-46))(ζ^10-ζ^(-10))(ζ^18-ζ^(-18))
-(ζ^64-ζ^(-64))(ζ^38-ζ^(-38))(ζ^4-ζ^(-4))
=ζ^74-ζ^38-ζ^54+ζ^18-ζ^(-18)+ζ^(-54)+ζ^(-38)-ζ^(-74)
-ζ^106+ζ^98+ζ^30-ζ^22+ζ^(-22)-ζ^(-30)-ζ^(-98)+ζ^(-106)
=ζ^74+ζ^218+ζ^234+ζ^18+ζ^162+ζ^306+ζ^322+ζ^106
-ζ^106+ζ^98+ζ^30+ζ^202+ζ^338+ζ^150+ζ^82-ζ^74
=(ζ^98+ζ^218+ζ^338)+(ζ^82+ζ^202+ζ^322)+(ζ^30+ζ^150)
+(ζ^18+ζ^162+ζ^234+ζ^306)
=(ζ^98+ζ^218+ζ^338)+(ζ^82+ζ^202+ζ^322)+(ζ^30+ζ^150+ζ^270)
+(ζ^18+ζ^90+ζ^162+ζ^234+ζ^306)-(ζ^90+ζ^270)
=ζ^98(1+ω+ω^2)+ζ^82(1+ω+ω^2)+ζ^30(1+ω+ω^2)
+ζ^18(1+ξ+ξ^2+ξ^3+ξ^4)-ζ^90(1-1)
=0．
よって， S=0すなわち sin∠DEC・sin∠EBA・sin∠BDF=sin∠CEB・sin∠ABD・sin∠FDEとなり，
チェバの定理の三角関数表現の逆により，３直線 EC,BA,DFは１点で交わる．
したがって，点Aは直線DF上にあり， ∠BDA=∠BDF=18°．
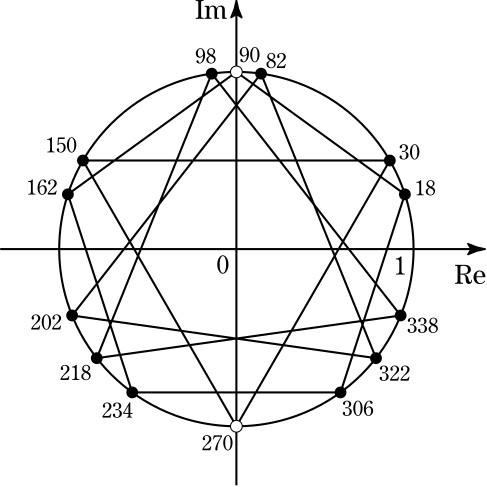※1の原始360乗根ζを用いた上記の計算は，右図のような複素平面上の12個の黒丸が表す複素数の和が0になることを意味していますが，２つの白丸を加えた14個の点が，原点を中心とする３つの正三角形と１つの正五角形の頂点を形成していることが，本問が整角四角形として成立しているポイントとなっています．
初等幾何による証明
本問は，1970年代にJ.F.Rigbyが整角四角形の初等幾何による証明を体系的に探して以来，「初等幾何による証明が見つかっていない」とされていた問題群の１つですが，2015年10月にaerile_re氏によって全ての整角四角形問題に適用可能な証明方法が発見されたことにより，本問を含む問題群も初等幾何で証明可能となりました．その手法「外心３つ法」の詳細は，雑誌「現代数学」2016年2月号の連載記事「数学パズルにトドメをさす？！」にて紹介させて頂いています．
同記事は，2018年9月発売「パズルな数学・数学なパズル 数学パズルにトドメをさす？！ 第１集」（現代数学社）にも収録しています．
aerile_re氏により最初に発表された証明はこちら．（Yahoo知恵ノートサービス終了のため、アーカイブへのリンクです）
|